质数筛小记
本篇博客详细解析 LeetCode 204(Count Primes)的三种解法,包括枚举法、埃氏筛和欧拉筛(线性筛),并分析其时间复杂度与空间复杂度。
前言
题目出自leetcode 204,本质上是为了筛选出小于n的所有质数。三种方法:
- 暴力枚举
- 埃氏筛
- 欧拉筛(线性筛)
枚举法
枚举法中我们只需要从 2 到 n 判断每个数是否质数即可。对于第 i 个数来说判断是否质数,只需要看其能否被 2 到 i-1 整除,如果有可以整除的则为合数,不能整除则为质数。
进一步优化,考虑到如果 y 是 x 的因数,那么 x/y 也必然是 x 的因数,因此我们只要校验 y 或者 x/y 即可。而如果我们每次选择校验两者中的较小数,则不难发现较小数一定落在 [2, sqrt(x)] 的区间中,因此我们只需要枚举 [2, sqrt(x)] 中的所有数即可。
时间复杂度:O(n*sqrt(n))
空间复杂度:O(1)
埃氏筛 Sieve of Eratosthenes
考虑质数 x,那么 x 的倍数一定是合数,因此可以将 2x、3x….这些 x 的倍数都标记为合数,如此一来,之后遇到这些数的时候就直接知道他们是合数,直接跳过即可。
进一步优化,不用从 2x 开始标记,而是从 x*x 开始标记,因为 2x 之前已经被 2 标记过,3x 已经被 3 标记过…
时间复杂度:O(n * logn * logn)
空间复杂度:O(n)
欧拉筛(线性筛)
在埃氏筛当中,许多合数会被重复标记,比如 6 会被 2 和 3 标记,15 会被 3 和 5 标记。由于一个合数很可能会被分解成多个不相同的质数的乘积,如 42 = 2 * 3 * 7,那么 42 就会被标记三次,造成时间复杂度上的浪费。
在欧拉筛的优化中,观察到每个合数被分解为质数乘积后,就拿 42 = 2 * 3 * 7 举例,必然存在一个最小的质数因子,这里是 2,比如 15 = 3 * 5 中的最小质数因子是3,因此欧拉筛的核心在于,让每个合数只被最小的质数因子标记,这样一来就能避免被其它质数因子重复标记。
那么如何做到每个合数只被最小的质数因子标记呢?首先我们维护一个按从小到大顺序的质数数组 primes。然后写出伪代码:
1
2
3
4
5
6
7
8
isPrime = bool[n] // 大小为n,全部初始化为true
primes = int[0] // 大小为0
for i in 2..n:
if isPrime[i]:
primes.push_back(i)
for p in primes:
isPrime[i*p] = false
if (i%p == 0) break
首先对于任意一个数 i,可以表示成最小质因子 pi 乘上另一个数 num,即 i = pi * num,如 42 = 2 * 21,我们用 i 的倍数来标记后面的合数,这里的倍数因子从最小的质数开始遍历取得,当 i 被倍数因子整除,就停止使用 i 更大的倍数标记。
这里的核心在于,由于 i 的最小质因子是 pi,当 p 不能整除 i 时,说明 p < pi(因为 p 是从最小的质数开始获得的),那么对于 j = i * p,我们有 j 的最小质因子肯定是 p,因此我们做到了 j 被最小质因子标记。当遍历到的 p 第一次能整除 i 的时候,说明 p == pi,倘若不终止循环,下一个遍历到的 p 会大于 pi,对于此时的 j = i * p 中的p 就不再是 j 的最小质因子,此时 j 被最小质因子标记了一次,又被 p 标记了一次,导致重复标记。因此当 p 能整除 i 的时候终止遍历,就做到了 j 不会被非最小质因子标记。
时间复杂度:O(n)
空间复杂度:O(n)
多线程の埃氏筛
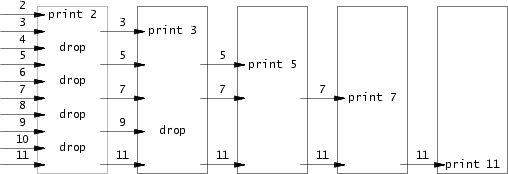
借用rsc那篇文章里的图:
图中每个矩形可以看成一个线程/进程,每个线程负责处理一个质数,比如第一个线程负责过滤质数 2 的倍数,第二个线程负责过滤质数 3 的倍数。
一开始只有最左边的线程(第一个线程),我们将 2 到 n 全部输入这个线程,输入的第一个数就是这批数里的最小质数,那么该线程就负责处理这个质数,然后将剩下未被过滤的数,作为第二个线程的输入,第二个以及后续的线程也执行同样操作。
这个多线程的埃氏筛实际上能不能提高效率我不知道,但可以确定的是,它在时间复杂度上其实是跟线性筛一样的,因为每个数只会被最小质因子过滤,不会输入到下一个线程中被重复处理。
说个题外话,可以看到图中线程之间就像管道一样,通过这个管道来传递数据。rsc在文章中想说明的是,这种并发编程风格不是为了效率,而是为了清晰。想象一下,线程之间的通信如果没有抽象成管道,而是共享内存,这种太过于low-level的表达方式,使得我们还要用一些同步工具+共享内存区域来表示这个通信过程。